Time Value of Money – Foundations of Finance

A fundamental concept in finance is that there is a time value of money. That is to say that an amount of money received today is worth more than the same amount of money received in a year’s time or any time in the future. While this principle may be difficult to grasp for those who are new to finance (“How can €1,000 today be different to €1,000 in 12 months’ time?”), it is a core building block when assessing business (and personal) finance decisions. The purpose of this post will be to explain the underlying concept, to introduce some real life examples of where time value of money concept applies and to examine the more technical computational elements associated with time value of money.
Why is there a time value of money?
There are a number of key reasons that, all else being equal, a sum of money received today is worth more than the same sum of money received some time in the future. Taking the example of receiving €1,000 today or in 2 years’ time we will take a look at each of the reasons below;
Opportunity Cost
By receiving the €1,000 today you can invest it and earn a return (e.g. interest in bank), resulting in a higher value in the future. However, if you only receive the €1,000 in 2 years’ time you cannot begin to accumulate interest until then. This lost opportunity to earn interest/return is the opportunity cost (i.e. the benefit foregone from delayed receipt of the cash).
Inflation/Purchasing Power
The purchasing power of the sum of money is also an important factor. What you can buy today for €1,000 may not be the same as what you can buy in 2 years’ time with the same amount of cash. Generally inflation (i.e. the general price of things) is positive (as opposed to deflation) and as such the purchasing power of your money is continuously being eroded. An extreme example might be housing – consider the type of house you could have bought with £50,000 (yes, pounds) 20/30 years ago compared to what the equivalent € amount (€63,500) could buy you today. The same amount of actual cash but vastly different purchasing powers.
Consumption Preference
Individuals typically prefer present consumption to future consumption. In order to forego current consumption, people would have to be offered more in the future to make it worthwhile delaying their consumption. Thus if the preference for current consumption (cashflow) is strong, an individual/business will place less value on future consumption (cashflows).
Risk
Receiving €1,000 today is certain, however receiving €1,000 in 2 years’ time comes with some risk (e.g. it won’t be paid or only part paid). Naturally the risk depends on who is making you the promise and your assessment of their ability to repay. The greater risk surrounding the future payment the less valuable that payment is in today’s terms. Thus a certain €1,000 today is worth more than a risky €1,000 in 2 years’ time.
Overall these four variables interact to determine the trade-off people/businesses use to assess future cashflows. The general relationships are as follows (and vice versa);
- Higher opportunity cost = lower value placed on future cashflows
- Higher expected inflation = lower value placed on future cashflows
- Greater preference for current consumption = lower value placed on future cashflows
- Greater risk in future cashflows = lower value placed on future cashflows
How does it work?
The method by which the above factors are incorporated into an analysis of the value of future cashflows is by something called the discount rate. The discount rate is a rate at which present and future cash flows are traded off – i.e. it is the rate that you can use to value future cashflows today. The discount rate can also be seen as your time value of money price or your opportunity cost (i.e. the return you require before it makes an investment worthwhile for you). The higher the discount rate is, the lower the value placed on future cashflows.
Note: The process by which businesses determine an appropriate discount rate to assess investments is an area in itself and is beyond the scope of this post. This area is called cost of capital and will be covered in CAP1 Finance also.
Calculation Basics
Any financial assessment of a business opportunity will involve projecting future cashflows and determining whether the project is worthwhile or not. One of the fundamental principles when doing a financial assessment of an investment opportunity is that you cannot simply add cashflows from different time periods together. Hopefully this makes sense to you after the previous sections – cashflows from different periods are not worth the same in today’s terms. In assessing potential opportunities with different cashflow patterns you must first value them all to a common time period – typically this is done in today’s value (also called Time Zero). Using the relevant discount rate, you “discount” the future cashflows back to their present values (i.e. their value in today’s money). Once they are all valued at the same point in time you can then add them together to get the total value of all future cashflows in today’s terms.
- To “discount” = To determine the value in today’s terms of cashflows received sometime in the future
- “Present Value” = The value of cashflows to be received in the future in today’s terms (e.g. How much is €50,000 received in 10 years’ time worth today? Its present value)
- “Future Value” = The amount of cash to be received at some time in the future.
- “Discount Rate” = The rate at which the future cashflow is discounted to get to its value today. Can also be called the required rate of return or cost of capital.
Taking a simple example of one cashflow in the future, the relationship between the future value and present value of the cashflow can be illustrated as follows;
Thus if the relevant discount rate for you/your business was 10% you would value €50,000 received in 4 years’ time as being equivalent to €34,150 today. You could also say that you would be indifferent between €34,150 today or €50,000 in 4 years’ time based on a 10% required return.
Note that the reverse relationship (i.e. getting from present value to future value) is something many of us will have come across before also;
This is essentially how savings accounts work – you start off with a lump sum (i.e. the present value) of say €10,000 and leave it in a savings account for 4 years with an interest rate of 10%. You can then use the above formula to calculate what the future value will be in 4 years’ time (ignoring tax etc.)
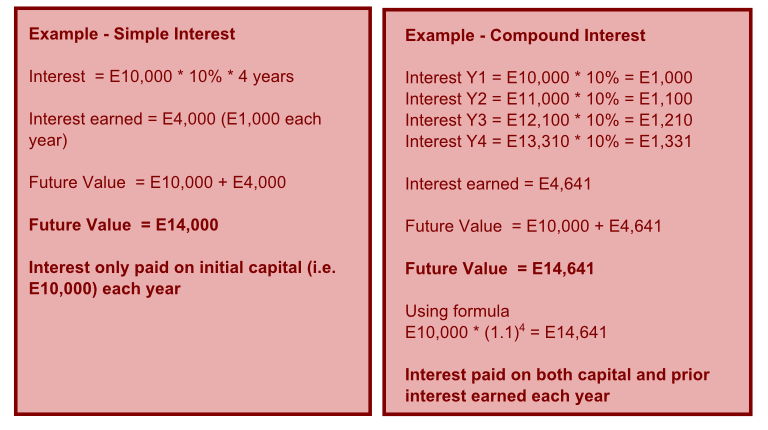
Simple vs. Compound Interest
There are two basic approaches to calculating interest – simple interest and compound interest. The most relevant one for real world applications would be compound interest, where interest is paid on both capital and previous interest earned/incurred.
Common Cashflow Patterns
Many assets in finance can be represented by one or a combination of the below cashflow patterns;
- Simple cashflows – as above, single or multiple individual cashflows;
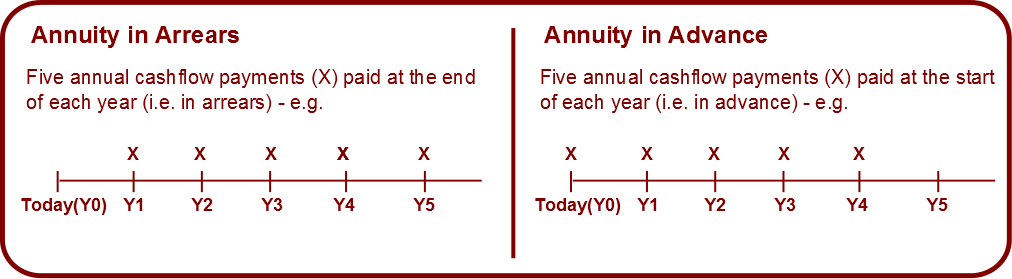
- Annuities – a set payment each year for an agreed number of years. Payments can be in advance or in arrears; and
- Perpetuities – a payment each year with no end date. Payments can be flat or growing by a constant rate each year.
A bond which pays off the capital amount at the end of its term would be made up of an annuity (interest payments each year) and a simple cashflow (i.e. repayment of capital at the end).
A mortgage would be an annuity type cashflow – with the same amount being paid off each period (ignoring variable interest rates for simplicity) for a set number of years.
A property could simplistically be valued as perpetuity – an annual rent payment received forever.
Annuities & Perpetuities
We will take a look at both annuities and perpetuities in more depth below. Both of these cashflow profiles are crucial in business finance and it is important that you fully understand the concepts and how to calculate the present value of each of them.
Annuities
An annuity is a series of equal cashflows over a set period of time. Examples include a lease and mortgage repayments. The concept of annuities is very important in finance in areas such as bond valuations and pensions. Annuities can be in arrears (where the first payment is made at the end of the first period) or in advance (where the first payment is made at the start of the first period). This distinction is important as it will impact how you determine the present value of the annuity.
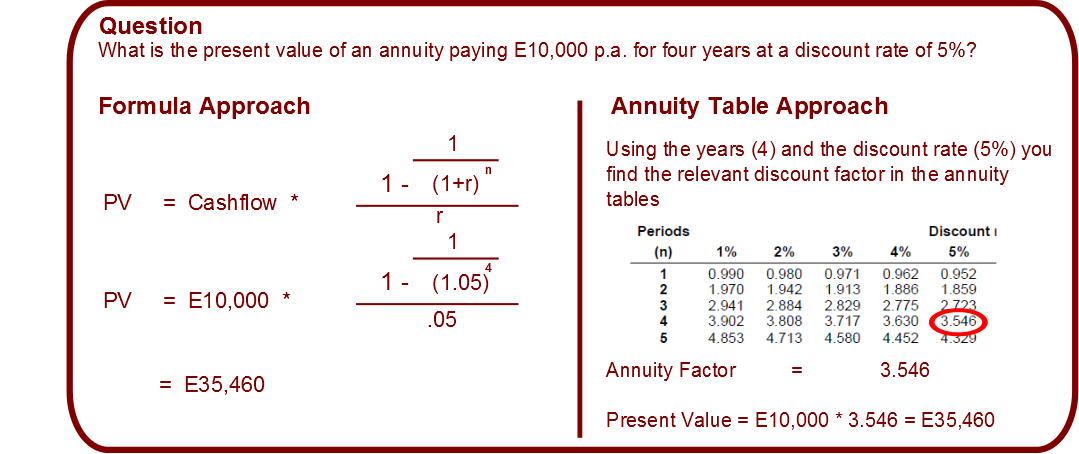
The following formula provides the present value of an annuity in arrears;
The discount tables (discussed in more detail below) provide all the annuity factors so you do not need to learn off the above formula however you should understand from first principles how the present value of an annuity is calculated – it is merely the sum of the relevant discounted single cashflows as the below example illustrates.
The below diagram also illustrates the key principle of the time value of money – while the nominal amount (i.e. before any discounting) of cashflow of this annuity is €40,000 (i.e. €10,000 over 4 years) its present value (i.e. its value in today’s terms) is much less and each annual cashflow is worth less in today’s terms the further out you go.
Perpetuity
A perpetuity is essentially a form of annuity with no end date. Thus the payments never finish and continue forever. You may now think that it would be impossible to value such a cashflow pattern as the cashflows never stop and thus its value must be infinite. However, the further out the cashflows are the less valuable they are today (as we saw in the chart in the previous section) and there comes a point when the discounting of the future cashflows means it is of negligible value in today’s terms. The excel file attached at the bottom of this post has a perpetuity calculator (see panel 3.1 & 3.2) and also includes the proof that the further out the cashflows are the less valuable they are in today’s terms.
As with an annuity there is a shortcut formula to determine the present value of all the cashflows of a perpetuity assuming the cashflows remain constant each year. However, it is common in many areas of finance not to look at a constant payment perpetuity but a perpetuity with a constantly growing cashflow (e.g. growing at 2% per annum). Similar to the flat payment perpetuity, you can mathematically summarise (you don’t need to know the detail) all those future cashflows into the following formula to determine its present value. This formula will be particularly important when you start looking at the area of cost of capital and company valuations.
You can use the excel file at the bottom of this page to try your own variations of the perpetuities and sense check the present value solutions you come up with.
Discount Tables – Use & Explanation
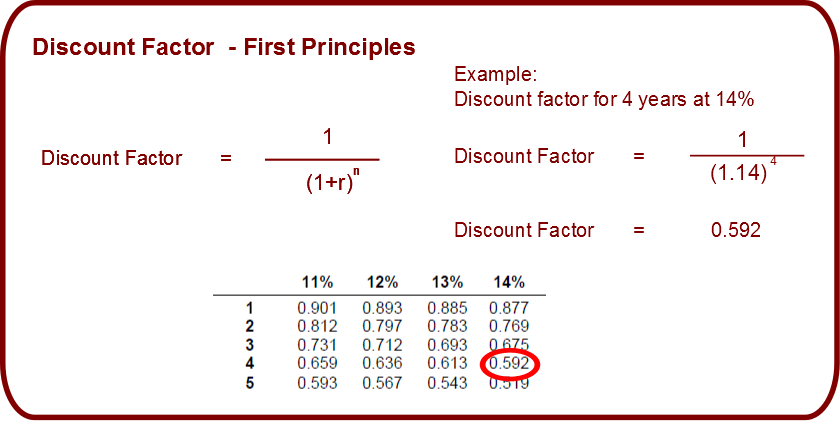
Much of the computational side of time value of money can be repetitive and time consuming in an exam. In most finance exams students are provided with “discount tables” to assist them in speeding up their calculations. While these tables are very useful for students and it is important that you understand how to use them, you should avoid being over reliant on the tables and you need to ensure you understand the first principles by which the factors in the tables are actually calculated.
The two main tables we will look at here are (1) Present Value Table (PVT); and (2) Annuity Table (AT).
(1) Present Value Table (PVT)
The PVT provides a shortcut to determine the appropriate factor by which to multiple future cashflows to get their present values. Thus instead of using the normal formula as outlined below, you take the discount rate (e.g. 6%) and the number of years (e.g. 5) and you find the relevant factor in the PVT and then multiple it by the relevant cashflow.
Note: there may be slight rounding discrepancies when using the PVT (As can be seen above) but as long as you approach is clear to the examiner you should be rewarded the marks.
It is important to understand where these discount factors are coming from as the PVT will be of no use in an exam should a discount rate of, say, 8.5% come up (which examiners can do intentionally from time to time).
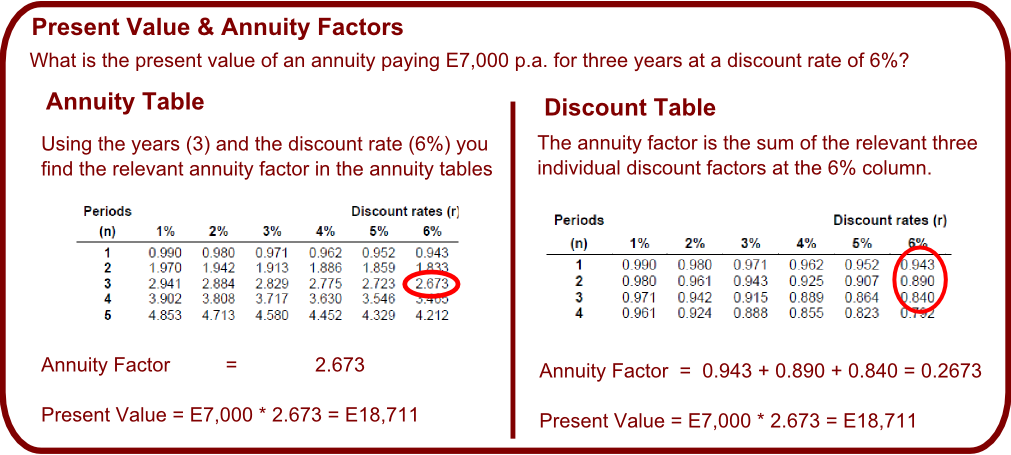
(2) Annuity Table (AT)
The AT has a similar logic to the PVT in that you take the discount rate and number of years and find the relevant factor (typically called an annuity factor) to multiply to the cashflow (remember that an annuity has the same cashflow each year). You can calculate the present value of an annuity using the formula discussed above or the AT – both methods are shown below.
Understanding the formula for the present value of annuities is not as important as PVT however one key point to understand is the relationship between the factors in the PVT and AT. As previously discussed above, an annuity is can be seen as a series of individual cashflows. Thus when determining the annuity factor, you can just add all the relevant individual discount factors from the PVT together to get the annuity factor in the AT.
Summary
The time value of money concept is a fundamental pillar across all of personal and business finance. From investment appraisal, company valuations, raising finance and pension planning, it has endless applications and students must ensure that they are comfortable with the underlying concept, the basics of discounting cashflows and the more detailed typical cashflow patterns that arise in a business finance context.
Excel TVOM Calculators
The attached excel file below provides a number of different calculators to assist you in understanding the core time value of money principles. These include;
1.1 Present value calculator
1.2 Future value calculator
2.1 Present value of annuity (in arrears) calculator (including proof from first principles)
2.2 Present value of annuity (in advance) calculator (including proof from first principles)
3.1 Present value of perpetuity (no growth) calculator (including proof from first principles)
3.2 Present value of perpetuity (with growth) calculator (including proof from first principles)
4.1 Discount/annuity factors calculators
Students can use these calculators to understand how the various calculations work and also attempt questions and check your answers












no comments